Hello friends, in this post I want to share: Calculation of the Metric Helical Bevel Gear.
This is a topic that has been asked frequently on my YouTube channel and despite not having had the opportunity to manufacture a gear with these characteristics, I decided to task of consulting, understanding, and explaining this topic at least the theoretical part, and in this post, I want to convey it to you. So without further ado, let’s start!
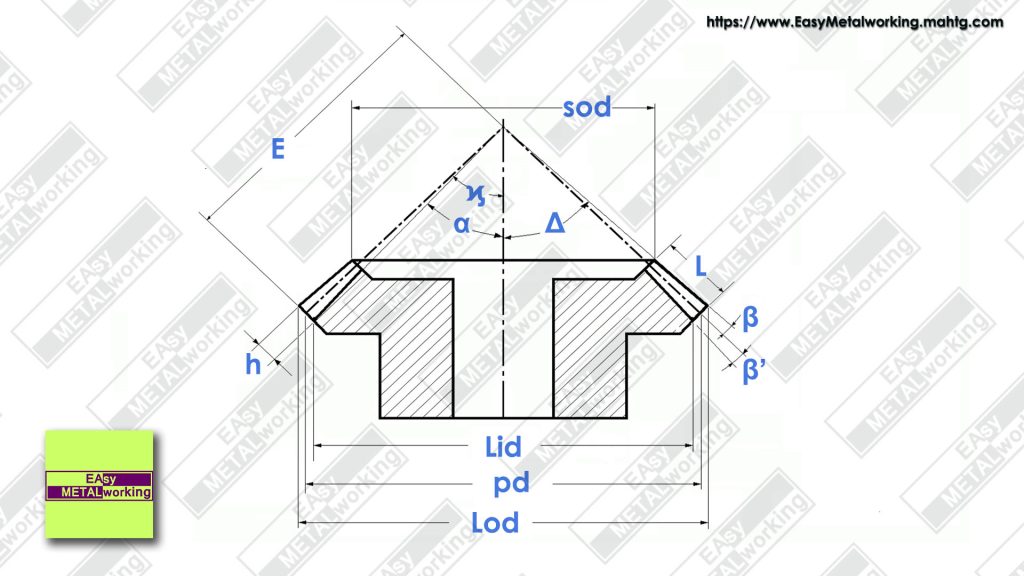
Known Data:
- m: Metric Gear Module.
- z: Number of Teeth.
- α: Pitch Angle.
- L: Face Width.
- Ω: Gear Helix Angle.
- Cl: Chordal thickness of the cutter on the pitch circle, at the larger end of the gear.
- Cs: Chordal thickness of the cutter tooth on the pitch circumference, at the smaller end of the gear.
Formulas for Bevel Gear
These are the machining formulas for the Bevel Gear:
- Apparent module (am)
am = m / cos Ω - Pitch diameter (pd)
pd = am * z - Larger outside diameter (Lod)
Lod = pd + (2 * m * cos α) - Cone distance (E)
E = pd / (2 * sin α ) - Larger inside diameter (Lid)
Lid = pd – (1.157 * 2 * m * Cos α) - Smaller outside diameter (sod)
sod = Lod (E – L) / E - Tooth height (h)
h = 2.167 * m - Angle corresponding to the module (β)
tan β = m / E - Angle corresponding to the bottom of the toothing clearance (β’)
tan β’ = 0,157 (m / E) - Half angle of the face cone (Δ)
Δ = α + β - Dividing Head Tilt Angle (ϗ)
ϗ = α – (β + β’) - Lead (L)
L = π * pd / tan Ω
EXAMPLE:
Make the Calculation of the Metric Helical Bevel Gear with the following data:
- Metric Module (m) = 4
- Number of teeth (z) = 16
- The angle at the center of the gear (α) = 37° 20′
- Face Width (L) = 19 millimeters
- Gear helix angle (Ω) = 30°
- The chordal thickness of the cutter on the pitch circle, at the larger end of the gear (Cl) = 5.8 millimeters
- The chordal thickness of the cutter tooth on the pitch circumference, at the smaller end of the gear (Cs) = 4.3 millimeters
These last two values: Cl and Cs are taken from the respective cutters. I will talk about this topic later.
Now let’s go with the calculations:
In the first instance, we will calculate everything related to the geometry of the bevel gear, which does not differ much from the metric bevel gear with straight teeth.
- Apparent module (am)
am = m / cos Ω
am = 4 / cos 30°
am = 4 / 0.86603
am = 4.618 - Pitch diameter (pd)
pd = am * z
pd = 4.618 * 16
pd = 73.90 millimeters. - Larger outside diameter (Lod)
Lod = pd + (2 * m * cos α)
Lod = 73.90 + (2 * 4 * cos 37° 20′)
Lod = 73.90 + (2 * 4 * 0.7951)
Lod = 73.90 + (2 * 3.1804)
Lod = 73.90 + 6.3609
Lod = 80.264 millimeters - Cone distance (E)
E = pd / (2 * sin α )
E = 73.90 / (2 * sin 37° 20′)
E = 73.90 / (2 * 0.60645)
E = 73.90 / 1.21290
E = 60.92 millimeters - Larger inside diameter (Lid)
Lid = pd – (1.157 * 2 * m * Cos α)
Lid = 73.90 – (1.157 * 2 * 4 * Cos 37° 20′)
Lid = 73.9 – (1.157 * 2 * 4 * 0.7954)
Lid = 73.9 – (1.157 * 2 * 3.1816)
Lid = 73.9 – (1.157 * 6.3632)
Lid = 73.9 – 7.3622
Lid = 63.537 millimeters - Smaller outside diameter (sod)
sod = Lod (E – L) / E
sod = 80.26 (60.92 – 19) / 60.92
sod = 80.26 (41.92) / 60.92
sod = 3,364.4992 / 60.92
sod = 55.29 millimeters. - Tooth height (h)
h = 2.167 * m
h = 2.167 * 4
h = 8.668 millimeters - Angle corresponding to the module (β)
tan β = m / E
tan β = 4 / 60.92
tan β = 0.065659
β = tan⁻¹ 0.065659
β = 3.7566°
β = 3° 45′ 23.91″ - Angle corresponding to the bottom of the toothing clearance (β’)
tan β’ = 0,157 (m / E)
tan β’ = 0,157 (4 / 60.92)
tan β’ = 0.157 * 0.065659
tan β’ = 0.010308463
β’ = tan⁻¹ 0.010308463
β’ = 0.590610°
β’ = 0° 35′ 26.19″ - Half angle of the face cone (Δ)
Δ = α + β
Δ = 37° 20′ + 3° 45′
Δ = 41° 5′ - Dividing Head Tilt Angle (ϗ)
ϗ = α – (β + β’)
ϗ = 37° 20′ – (3° 45′ + 0° 35′)
ϗ = 37° 20′ – 4° 20′
ϗ = 33° - Lead (L)
L = π * pd / tan Ω
L = (3.1416 * 73.9) / tan 30°
L = 232.164 / 0.57735
L = 402.119 millimeters
With these data, it is possible to carry out the turning part, the inclination of the dividing head, and search for the series of gears in the banjo to mount on the universal milling machine.
As a second step, we go with the calculation of the angle of rotation of the dividing head and the deviation for the correct cutting of the teeth of the helical bevel gear.
Machining formulas:
- Tooth Variation Coefficient (Χ)
X = (E – L) / E - Milling cutter module (mc)
mc = X * m - Equivalent helical pitch diameter (Pd)
Pd = pd / cos α - Number of teeth of the equivalent helical gear (eZ)
eZ = Pd / (m * Cos² Ω) - The apparent pitch at the larger end of the gear (ap)
ap = π * m / Cos Ω - Pitch taper radius at the larger end of the gear (TR)
TR = pd / (2 * Sin α) - The rotation angle of the gear (ra)
ra = (57.3 / pd)*((ap/2) – (TR / (L * Cos Ω) * (Cl – Cs))) - Divisions in the dividing head of the milling machine: (Dd)
Dd = 40 / z
40 is the dividing head ratio - Number of degrees for a full rotation of the dividing head (Nd)
Nd = 9° - Dividing head holes (dhh)
dhh = q * (ra / Nd) - Readjustment calculation (Rc)
Rc = (Cl / 2 * Cos Ω) – ((Cl – Cs) * TR / 2 * L * cos Ω)
Now apply the previous formulas in the example:
- Tooth Variation Coefficient (Χ)
X = (E – L) / E
X = (60.92 – 19) / 60.92
X = 41.92 / 60.92
X = 0.688 - Milling cutter module (mc)
mc = X * m
mc = 0.688 * 4
mc = 2.75 - Equivalent helical pitch diameter (Pd)
Pd = pd / cos α
Pd = 73.90 / cos 37° 20′
Pd = 73.90 / 0.7954
Pd = 92.909 millimeters - Number of teeth of the equivalent helical gear (eZ)
eZ = Pd / (m * Cos² Ω)
eZ = 92.9 / 4 * Cos ² 30°
eZ = 92.9 / 4 * 0.86603 ²
eZ = 92.9 / 4 * 0.75
eZ = 92.9 / 3
eZ = 30.96 For the Number of teeth of the equivalent helical gear Zf, cutter number 5 corresponds - The apparent pitch at the larger end of the gear (ap)
ap = π * m / Cos Ω
ap = 3.1416 * 4 / cos 30°
ap = 3.1416 * 4 / 0.86603
ap = 12 .5664 / 0.86603
ap = 14.5103 - Pitch taper radius at the larger end of the gear (TR)
TR = pd / (2 * Sin α)
TR = 73.90 /(2 * Sin 37° 20′)
TR = 73.90 /(2 * 0.60645)
TR = 73.9 / 1.2129
TR = 60.928
Here is a small parenthesis. The value “Cl” cordal thickness of the cutter on the pitch circle, at the larger end of the gear, is taken in the milling cutter with a special gauge, or it can be done approximately with a conventional vernier, and in this case, it is done in the milling cutter module 4, and the value is 5.8 millimeters,
In the same way, for the chordal thickness of the cutter on the pitch circle, at the smaller end of the gear.: “Cs” is made in the cutter module 2.75 that We calculated in the point: “cutter Module and that gave a value: of 2.75 and whose value is: 4.3 millimeters.
- The rotation angle of the gear (ra)
ra = (57.3 / pd)*((ap/2) – (TR / (L * Cos Ω) * (Cl – Cs)))
ra = 57.3 / 73.9 ((14.51/2) – (60.92/19 * Cos 30°)(5.8 – 4.3))
ra = 0.775 (7.25 – (60.92/19 * 0.86603) * 1.5)
ra = 0.775 (7.25 – (60.92/16.45) * 1.5)
ra = 0.775 (7.25 – (3.703 * 1.5))
ra = 0.775 (7.25 – 5.55)
ra = 0.775 (1.7)
ra = 1.31
- Divisions in the dividing head of the milling machine: (Dd)
Dd = 40 / z
Dd = 40/16
Dd = 2 turns, 1 hole in the plate of 2 holes. Now amplifying the fraction by 14 times
Dd = 2 turns, 14 holes in the plate of 28 holes. - Number of degrees for a full rotation of the dividing head (Nd)
Nd = 9° - Dividing head holes (dhh)
dhh = q * (ra / Nd)
dhh = 28 * (1.31 / 9°)
dhh = 28 * 0.145
dhh = 4.06 holes or 4 holes of the dividing head plate. - Readjustment calculation (Rc)
Rc = (Cl / 2 * Cos Ω) – ((Cl – Cs) * TR / 2 * L * cos Ω)
Rc = (5.8/2*Cos 30°) – ((5.8- 4.3) *60.92/219cos 30°)
Rc = (5.8/20.86603) – ((1.5)60.92/38*0.86603)
Rc = (5.8/1.73) – (91.38/32.9)
Rc = 3.35 – 2.77
Rc = 0.58 millimeters.
For gear milling it is recommended:
When we have to do the Calculation of the Metric Helical Bevel Gear, we must keep in mind:
- Tilt the dividing head 33° and set the dividing for 2 turns, 14 holes on the 28-hole plate.
- Assemble the gear train,
- Place the milling head vertically and mount the Modular spike cutter,
- Mill the teeth to the depth in the largest diameter of 8.7 mm.
- Rotate the piece clockwise with the head to the left 4 holes,
- move the table outward 0.6 millimeters, and mill the faces of the teeth.
- Rotate the part counterclockwise 8 holes and move the table 1.2mm to mill the faces of the teeth.
You may be interested in How to Copy a Metric Helical Gear
With this information, I hope to have explained the best way the features, concepts, and information about the Calculation of the Metric Helical Bevel Gear
If you think this note can help you or has been useful, I ask you to please vote with the highest star rating at the bottom of this article.
Thank you very much!
Please, subscribe to my YouTube Channel!