In this post I want to share you How to read a vernier calliper in fractional inches, Welcome!

Reading a vernier caliper in fractional inches is simple once the units in which it is divided are mastered and understood.
However, we must take into account that we work in fractions of an inch, and these are subdivided into smaller expressions and that these subunits are also expressed as a fraction.
So, this article is structured in four parts:
Part 1: understanding the inch,
Part 2: understanding the sub units of the Inch.
Part 3: understanding the vernier vernier in Inches.
Part 4: reading examples.
- Understanding the inch:
An inch is divided into 16 equal parts. If you take a part of these 16 you get a fraction: 1 / 16in. Therefore, 16 parts each of 1/16, joined or added together will result in 16/16.
Now, if the previous fraction is given a basic operation such as division, that is, if 16 is divided by 16, the result is 1; 1 inch.
But, why a division?
Simply because the fractions are a division, yes, a division of the numerator versus the denominator, understanding that the numerator is the number that is in the upper part of the fractional and denominator is the number that is below the fractional.
With these basic concepts of fractionaries we can understand a little better the management and the reading of fractions of the vernier in inches.
THE VALUES OF THE VERNIER IN FRACTIONAL INCHES
As stated earlier, if you take 1 part of the 16 in which the inch is divided, you get 1/16. If 2 parts are taken means that 1/16 should be added 1/16
To add two fractions, you must first observe their denominators, if denominators are equal, the result of add will be another fractionary with same denominator, in this case, the denominator of the two fractions is 16, that is, the fractional result will have as denominator 16.
Now, we proceed to operate the numerators of the two fractions, So then add 1 + 1 result is 2, so the total value of add 1/16 + 1/16 is 2/16.
2/16 is a number that can be simplified, then, taking halves in numerator we get 1 and again, taking half in denominator we get 8, therefore, after simplifying 2/16 an equivalence is obtained; 2/16 is equivalent to 1/8.
All the fractionaries of the vernier calliper in inches are SIMPLIFIED!
Now we go with the third fractionary, remember that there are 16 fractionaries that make an inch in the vernier calliper.
The third fractionary is then add to 1/8 1/16
To add two fractions and correct the read a vernier calliper in fractional inches First, the denominators must be observed, in this case, the denominators are NOT the same, therefore the addition can not be made directly as in the previous case. But this is not a matter of worry.
In order not to complicate the exercise much, I will work with the concept of fraction amplification.
1/8 + 1/16
First, you should observe the denominators of the two fractions and take the lower value, then the lowest value is 8 which belongs to 1/8 and taking advantage of that is an exact divisor of 16, we will multiply it or amplify it we have in such a way that we get instead of 8, 16 for this, you must multiply 1/8 by 2 in both the numerator and the denominator:
1/8 X 2 = 2/16.
Now you can add the fractional as they have the same denominator:
2/16 + 1/ 16
And it applies again the same process that in the first sum is left the same denominator, number 16 and add the numerators or the 2 and 1 which result is 3.
So, the value of the third fractional in inches in the vernier calliper is 3/16.
let´s go for the fourth fractional in the vernier calliper.
3/16 + 1/16 = 4/16, and simplifying is 1/4
let´s go for the fifth fractional in the vernier calliper:
1/4 + 1/16 = 5/16
The Sixth fractional is add to the previous 1/16
5/16 + 1/16 = 6/16 and simplifying is 3/8
The Seventh fractional is add to the previous 1/16
3/8 + 1/16 = 7/16
The Eighth fractional is add to the previous 1/16
7/16 + 1/16 = 8/16 and simplifying is 1/2
The Ninth fractional is add to the previous 1/16
1/2 + 1/16 = 9/16
The Tenth fractional is add to the previous 1/16
9/16 + 1/16 = 10/16 and simplifying is 5/8
The Eleventh fractional is add to the previous 1/16
5/8 + 1/16 = 11/16
The Twelfth fractional is add to the previous 1/16
11/16 + 1/16 = 12/16 and simplifying is 3/4
The Thirteenth fractional is add to the previous 1/16
3/4 + 1/16 = 13/16
The Fourteenth fractional is add to the previous 1/16
13/16 + 1/16 = 14/16 and simplifying is 7/8
The Fifteenth fractional is add to the previous 1/16
7/8 + 1/16 = 15/16
The Sixteenth fractional is add to the previous 1/16
15/16 + 1/16 = 16/16 = 8/8= 4/4 = 2 /2 = 1 inch.
As I said at the beginning, an inch is equivalent to 16/16
Vernier of the vernier calliper
The vernier of the vernier calliper divides a 1/16 in 8 equal parts , this is:
(1/16) / 8
In order to divide a fractional by a whole number, becomes the whole number to fractional. This is accomplished adding to the whole a denominator and the value to be always added is the unit or is the number one (1).
8 = 8/1
Now it is possible to make the division of two fractional numbers.
Divide 1/16 by 8/1
and proceed to perform the operation
Turn the second fraction upside down (reciprocal)
1/16 X 1X8 (reciprocal)
now Multiply the first fraction by that reciprocal
1/128
and Simplify the fraction (if needed)
the result is 1/128
In the vernier calliper in inches, the smallest unit you can get is 1/128 inch.
1/128+1/128 = 2/128 =1/64
1/64+1/128 = 3/128
3/128+1/128= 4/128 = 2/64 = 1/32
1/32 + 1/128 = 5/128
5/128 + 1/128 = 6/128 = 3/64
3/64+1/128= 7/128
7/128+1/128= 8/128= 4/64=2/32 = 1/16
in conclusion 8/18 is equivalent to 1/16 inch.
Rules for taking readings from the vernier calliper
- Count the positions in the rule before the zero of the vernier.
- verify the division of the vernier that matches exactly a division of the ruler in inches.
- If the first or the third or the fifth or the seventh division of the vernier coincides with one of the rule, then the number of divisions of the rule that are before the zero of the vernier by 8 is multiplied. If the first division of the vernier coincides with one of the rule is added 1, if the third division of the vernier coincides with one of the rule is added 3, if the fifth division of the vernier coincides with one of the rule is added 5 and if the seventh division of the vernier coincides with one of the rule is added 7,the previous value is the fractional numerator, the denominator is 128.
4.If the second or the Sixth divsion of the vernier coincides with one of the rule, then the number of divisions of the rule that are before the zero of the vernier by 4 is multiplied.If the second division of the vernier coincides with one of the rule is added 1 and if the sixth division of the vernier coincides with one of the rule is added 3,the previous value is the fractional numerator, the denominator is 64.
5.If the Fourth divsion of the vernier coincides with one of the rule, then the number of divisions of the rule that are before the zero of the vernier by 2 is multiplied and added 1. the previous value is the numerator of the fractional, the denominator is 32.
If in the fractional reading of the vernier calliper in inches the zero of the vernier passes from the number one of the rule, means that an inch has been exceeded therefore to the reading in fractions must be added the value indicated in the rule before the fractional.
Examples of Fractional Reading in Inches in the Vernier Calliper
3/4 in.
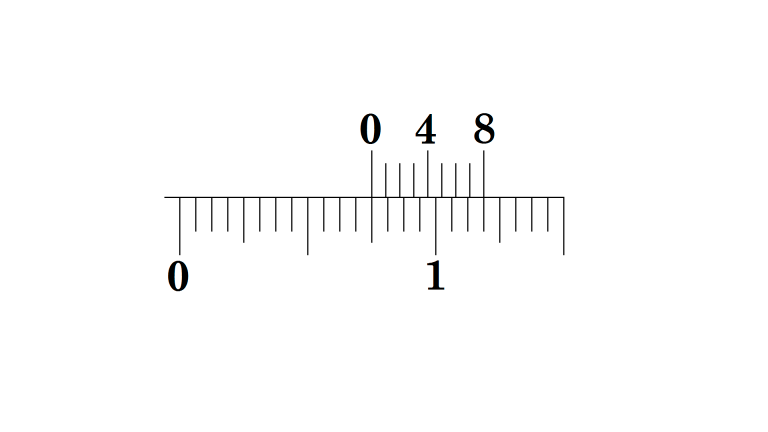
5/64 in.
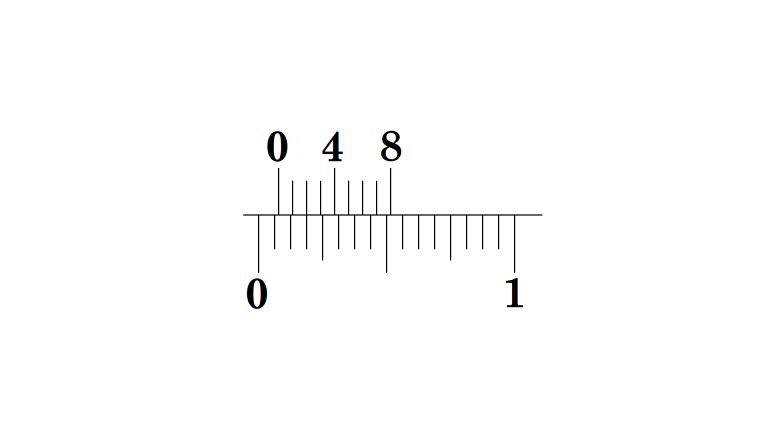
19/128 in.
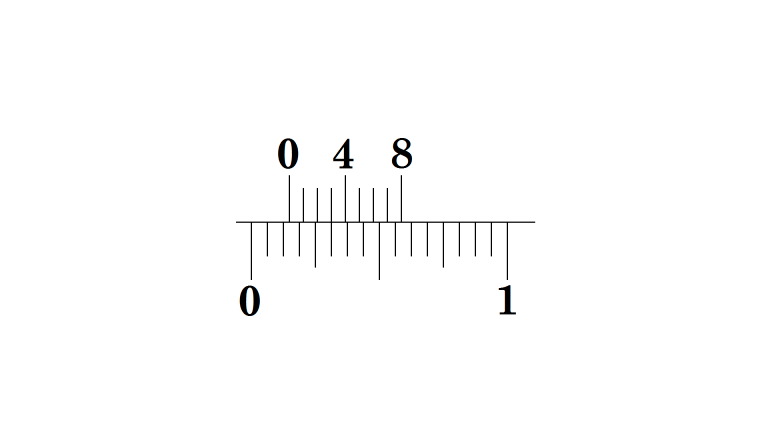
25/32 in.
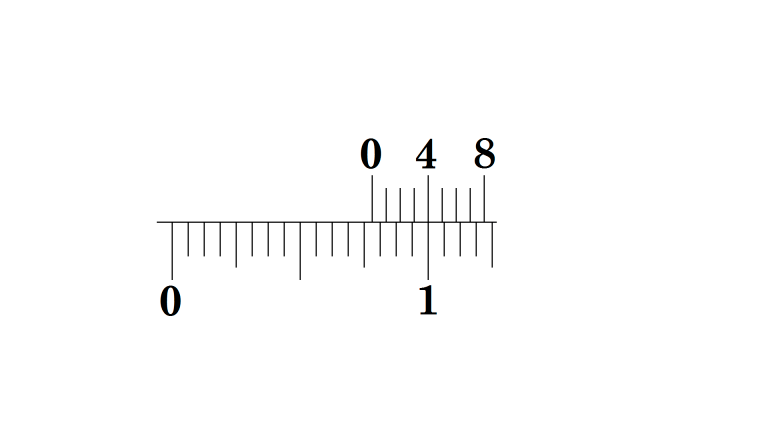
11/128 in.
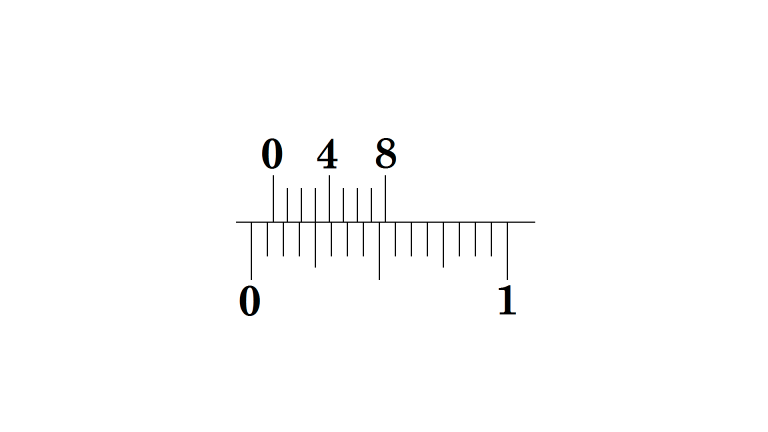
3/16 in.
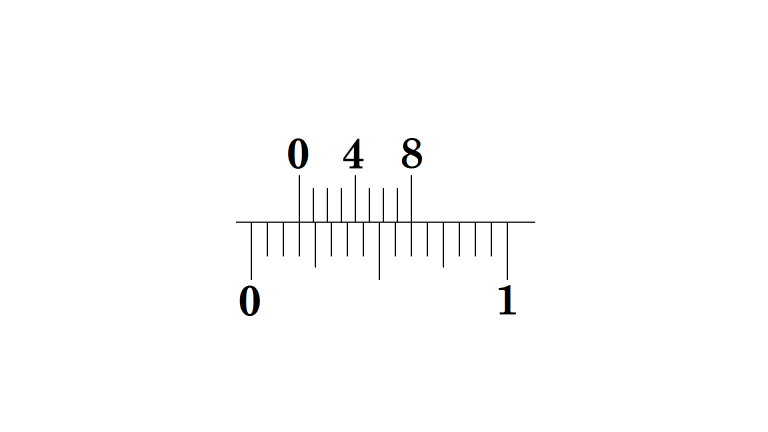
15/128 in.
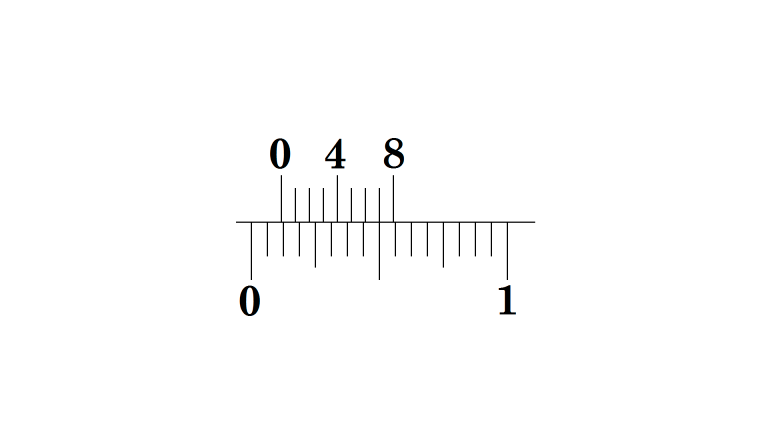
127/128 in.

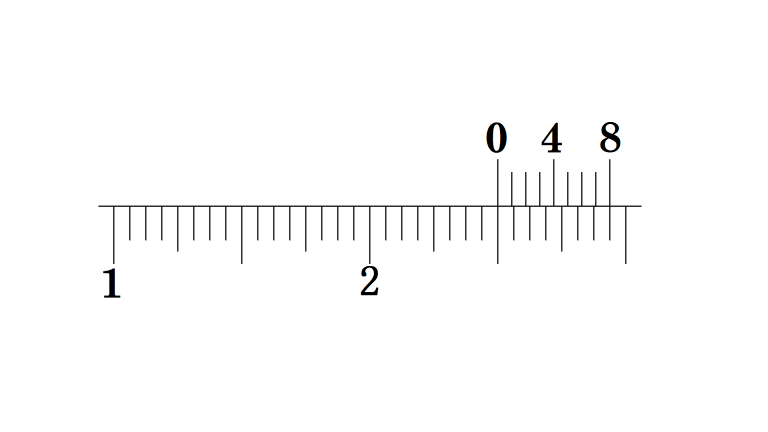
2 1/2 in.
If you liked the information you just delivered about How to Read a Vernier Calliper in Fractional Inches, then please help me with the rating that is below this post.
Thank you very much.
You might also be interested in: